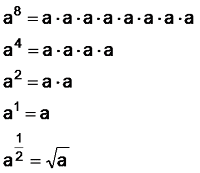Quadratische Ergänzung

Die quadratische Ergänzung ist ein Verfahren, das wir in zwei Fällen benutzen:

• Beim Lösen quadratischer Gleichungen
• Bei der Bestimmung der Scheitelpunktsgleichung quadratischer Funktionen

Lösen einer quadratischen Gleichung (allgemein)

  

Wer diese Formel auswendig kennt, hat seine Arbeit für alle Zukunft gemacht. Wer sie nicht kennt, muss die Herleitung halt in jedem konkreten Fall wieder neu machen. Wir mussten sie früher auswendig hinschreiben können. Wir hatten aber auch mehr Zeit und im Internat viel mehr Studium. Auch waren wir weniger abgelenkt - durch Dinge wie iPhones, Blogs, Facebook ...

Lösen eines konkreten Beispiels

 

Am meisten Mühe bereitet jeweils der Schritt von der zweiten zur dritten Zeile (die Hälfte von 2 nehmen und hinten das Quadrat davon abzählen). Wenn man das Binom zur Kontrolle wieder ausmultipliziert, stellt man fest, dass sich der Wert der linken Seite der Gleichung nicht geändert hat.

Ein weiteres Beispiel

Quadratische Ergänzung bei quadratischen Funktionen allgemein

Die Grundform (1. Zeile) informiert uns über den Öffnungsgrad der Parabel (hier 0.5 - eher weit offen) und über den y-Achsen-Schnittpunkt (hier 5.5 - x gleich null setzen).

Die quadratische Ergänzung liefert die Scheitelpunktsform, die uns über den Scheitelpunkt informiert (hier x = 3 und y = 1)

Hier noch das Schaubild, wie es der Taschenrechner (TI 89) liefert:

Hier die allgemeine Entwicklung der Scheitelpunktsform

Auch hier können die Koordinaten des Scheitelpunktes abgelesen werden.

Interessant wäre jetzt zu untersuchen, wie sich eine Änderung der Parameter a, b und c auf die Lage des Scheitelpunktes auswirken.

Dies dann ein anderes Mal.

Wurzeln - Theorie

Wer mit Potenzen umgehen kann, sollte auch mit Wurzeln keine Probleme haben, denn die Regeln sind die gleichen.

Betrachten wir die folgende Reihe.

Rechts ist jeweils die Wurzel gezogen worden. Dies entspricht der Division des Exponenten auf der linken Seite durch 2. Merken Sie sich vor allem die letzte Gleichung gut.

Hier eine zweite, ähnliche Reihenentwicklung:

Hier ist links jeweils die dritte Wurzel gezogen worden. Dies entspricht der Division des Exponenten rechts durch drei. Merken Sie sich wieder die letzte Gleichung gut.

Verallgemeinert gilt:

Noch einen Schritt weiter:

Verallgemeinert gilt also:



Und jetzt können wir die bekannten Potenzgesetze anwenden.

Multiplikation bei gleichem Radikand

Division bei gleichem Radikand

Multiplikation bei gleichem Wurzelexponent

Division bei gleichem Wurzelexponent

Binome - Theorie

Drei binomische Formeln sollte man unbedingt auswendig kennen. Man kommt leicht durch Ausmultiplizieren dazu.

Formeln

Und damit wäre es eigentlich getan, und Sie könnten zur Tagesordnung übergehen. Aber die Formeln müssen natürlich auch angewandt werden können. Und es ist so, dass gerade das dritte Binom oft verkannt wird, weil es nicht erkannt wird - anderen geht es halt im Leben auch oft so.

Anwendungsbeispiele

Aufgabe / Algebra / 16/22/a

Aufgabe / Algebra / 19/33/f

 

Die Beispiele zeigen, dass die Formeln sowohl von links nach rechts (ausmultiplizieren) als auch von rechts nach links (faktorisieren) angewandt werden können.

Merkregel für das 1. Binom z.B.

Das erste im Quadrat plus

Zweimal das erste mal das zweite plus

Das zweite im Quadrat

Vielleicht hilft eine geometrische Vorstellung beim Erinnern. Hier das erste Binom als Beispiel.

Man kann noch viele andere Formeln entwickeln.

Beispiel 1

 

Beispiel 2

Und dann gibt es da noch das Pascalsche Dreieck:

Ich glaube, Sie erkennen die Regel und können das Dreieck beliebig fortsetzen. Hier seine Anwendung Schritt für Schritt:

Das kann der Taschenrechner natürlich viel schneller.

Wählen Sie: F2 ... EXPAND