WILLKOMMEN auf meinem Matheblog.
Meine Posts finden Sie am besten über das ALPHABETISCHE PUBLIKATIONSVERZEICHNIS, über die LABELS oder über SUCHEN. Vielleicht hilft auch das BLOG-ARCHIV.
Der Internet Explorer wird wahrscheinlich den mit TeX geschriebenen Teil nicht richtig interpretieren und anzeigen.
Meine Posts finden Sie am besten über das ALPHABETISCHE PUBLIKATIONSVERZEICHNIS, über die LABELS oder über SUCHEN. Vielleicht hilft auch das BLOG-ARCHIV.
Der Internet Explorer wird wahrscheinlich den mit TeX geschriebenen Teil nicht richtig interpretieren und anzeigen.
31.05.2011
Wurzeln - Aufgabe
A / 59 / 170 / g
\[ \dfrac{\sqrt{1+\dfrac{1}{a}}} {a\cdot\sqrt[3]{\dfrac{1}{a}+\dfrac{1}{a^2}}} \] Wir machen im Zähler gleichnennrig und nehmen im Nenner das a unter die Wurzel. \[ \dfrac{\sqrt{\dfrac{a+1}{a}}} {\sqrt[3]{a^2+a}} \] Jetzt muss man wissen, dass gilt \[ \begin{align} \sqrt{x}&=x^\dfrac{1}{2}=x^\dfrac{3}{6}\\ \sqrt[3]{x}&=x^\dfrac{1}{3}=x^\dfrac{2}{6} \end{align} \] Darum können wir die Wurzelausdrücke mit Exponenten schreiben. \[ \dfrac{\left(\dfrac{a+1}{a}\right)^\dfrac{3}{6}} {\left(a^2+a\right)^\dfrac{2}{6}} \] Und das ist das gleiche wie \[ \dfrac{\left(\left(\dfrac{a+1}{a}\right)^3\right)^\dfrac{1}{6}} {\left(\left(a^2+a\right)^2\right)^\dfrac{1}{6}} \] Und dann mit einem der Potenzgesetze \[ \left(\dfrac{\left(\dfrac{a+1}{a}\right)^3} {\left(a\left(a+1\right)\right)^2}\right)^\dfrac{1}{6} \] \[ \left(\dfrac{\left(\dfrac{a+1}{a}\right)^2\left(\dfrac{a+1}{a}\right)} {\left(a\left(a+1\right)\right)^2}\right)^\dfrac{1}{6} \] \[ \left( \left(\dfrac {\dfrac{a+1}{a}} {a\left(a+1\right) }\right)^2 \dfrac{a+1}{a} \right)^\dfrac{1}{6} \] \[ \left( \dfrac {1} {a^4} \dfrac{a+1}{a} \right)^\dfrac{1}{6} \] \[ \left( \dfrac{a+1}{a^5} \right)^\dfrac{1}{6} \] \[ \sqrt[6]{ \dfrac{a+1}{a^5}} \]
\[ \dfrac{\sqrt{1+\dfrac{1}{a}}} {a\cdot\sqrt[3]{\dfrac{1}{a}+\dfrac{1}{a^2}}} \] Wir machen im Zähler gleichnennrig und nehmen im Nenner das a unter die Wurzel. \[ \dfrac{\sqrt{\dfrac{a+1}{a}}} {\sqrt[3]{a^2+a}} \] Jetzt muss man wissen, dass gilt \[ \begin{align} \sqrt{x}&=x^\dfrac{1}{2}=x^\dfrac{3}{6}\\ \sqrt[3]{x}&=x^\dfrac{1}{3}=x^\dfrac{2}{6} \end{align} \] Darum können wir die Wurzelausdrücke mit Exponenten schreiben. \[ \dfrac{\left(\dfrac{a+1}{a}\right)^\dfrac{3}{6}} {\left(a^2+a\right)^\dfrac{2}{6}} \] Und das ist das gleiche wie \[ \dfrac{\left(\left(\dfrac{a+1}{a}\right)^3\right)^\dfrac{1}{6}} {\left(\left(a^2+a\right)^2\right)^\dfrac{1}{6}} \] Und dann mit einem der Potenzgesetze \[ \left(\dfrac{\left(\dfrac{a+1}{a}\right)^3} {\left(a\left(a+1\right)\right)^2}\right)^\dfrac{1}{6} \] \[ \left(\dfrac{\left(\dfrac{a+1}{a}\right)^2\left(\dfrac{a+1}{a}\right)} {\left(a\left(a+1\right)\right)^2}\right)^\dfrac{1}{6} \] \[ \left( \left(\dfrac {\dfrac{a+1}{a}} {a\left(a+1\right) }\right)^2 \dfrac{a+1}{a} \right)^\dfrac{1}{6} \] \[ \left( \dfrac {1} {a^4} \dfrac{a+1}{a} \right)^\dfrac{1}{6} \] \[ \left( \dfrac{a+1}{a^5} \right)^\dfrac{1}{6} \] \[ \sqrt[6]{ \dfrac{a+1}{a^5}} \]
Erstellt von
Eugen Brigger
um
21:11
0
Kommentare

Diesen Post per E-Mail versendenBlogThis!In Twitter freigebenIn Facebook freigebenAuf Pinterest teilen
Labels:
A/059/170/g,
Algebra,
Aufgaben-gelöst,
BM,
Brüche,
Math,
Wurzeln
30.05.2011
Bruchrechnen - gelöste Aufgaben
Hier eine Aufgabe, die mir auch dazu dient, meine \(\TeX\) Fähigkeiten zu testen.
A / 27 / 64 / b
\[ \dfrac { \dfrac {1} {a-\dfrac {1} {a} } } { 1- \dfrac {1} {1-\dfrac {1} {1-\dfrac {1} {a} } } } \] Wir machen zweimal gleichnennrig. \[ \dfrac { \dfrac {1} {\dfrac {a^2-1} {a} } } { 1- \dfrac {1} {1-\dfrac {1} {\dfrac {a-1} {a} } } } \] Wir teilen zweimal durch einen Bruch (umstürzen und vermehren). \[ \dfrac { \dfrac {a} {a^2-1} } { 1- \dfrac {1} {1-\dfrac {a} {a-1} } } \] Wir machen wieder gleichnennrig. Im Zähler machen wir nichts. Und glücklicherweise wird meine \(\TeX\)-Formel etwas einfacher. \[ \dfrac { \dfrac {a} {a^2-1} } { 1- \dfrac {1} {\dfrac {a-1-a} {a-1} } } \] Wir vereinfachen. \[ \dfrac { \dfrac {a} {a^2-1} } { 1- \dfrac {1} {\dfrac {-1} {a-1} } } \] Wir schaffen ein lästiges Minuszeichen aus der Welt. \[ \dfrac { \dfrac {a} {a^2-1} } { 1- \dfrac {1} {\dfrac {1} {1-a} } } \] Wir dividieren durch einen Bruch im Nenner. \[ \dfrac { \dfrac {a} {a^2-1} } { 1+a-1} \] Wir vereinfachen den Nenner. \[ \dfrac { \dfrac {a} {a^2-1} } { a} \] Und schon sind wir durch. \[ \dfrac {1} {a^2-1} \] Die Aufgabe könnte auch mit der sogenannten Erweiterungsmethode gelöst werden \[ \dfrac { \dfrac {1} {a-\dfrac {1} {a} } } { 1- \dfrac {1} {1-\dfrac {1} {1-\dfrac {1} {a} } } } \] Wir erweitern den Bruch im Zähler und den Teilbruch im Nenner mit \(a\). \[ \dfrac { \dfrac {a} {a^2-a} } { 1- \dfrac {1} {1-\dfrac {a} {a-1 } } } \] Jetzt erweitern wir den Bruch im Nenner mit \((a-1)\). \[ \dfrac { \dfrac {a} {a^2-a} } { 1- \dfrac {a-1} {a-1-a} } \] Wir vereinfachen. \[ \dfrac { \dfrac {a} {a^2-a} } { 1- \dfrac {a-1} {-1} } \] Und vereinfachen nochmals. \[ \dfrac { \dfrac {a} {a^2-a} } {1-(1-a)} \] Und vereinfachen nochmals. \[ \dfrac { \dfrac {a} {a^2-a} } {a} \] Und schon sind wir wieder durch. \[ \dfrac {1} {a^2-1} \]
A / 27 / 64 / b
\[ \dfrac { \dfrac {1} {a-\dfrac {1} {a} } } { 1- \dfrac {1} {1-\dfrac {1} {1-\dfrac {1} {a} } } } \] Wir machen zweimal gleichnennrig. \[ \dfrac { \dfrac {1} {\dfrac {a^2-1} {a} } } { 1- \dfrac {1} {1-\dfrac {1} {\dfrac {a-1} {a} } } } \] Wir teilen zweimal durch einen Bruch (umstürzen und vermehren). \[ \dfrac { \dfrac {a} {a^2-1} } { 1- \dfrac {1} {1-\dfrac {a} {a-1} } } \] Wir machen wieder gleichnennrig. Im Zähler machen wir nichts. Und glücklicherweise wird meine \(\TeX\)-Formel etwas einfacher. \[ \dfrac { \dfrac {a} {a^2-1} } { 1- \dfrac {1} {\dfrac {a-1-a} {a-1} } } \] Wir vereinfachen. \[ \dfrac { \dfrac {a} {a^2-1} } { 1- \dfrac {1} {\dfrac {-1} {a-1} } } \] Wir schaffen ein lästiges Minuszeichen aus der Welt. \[ \dfrac { \dfrac {a} {a^2-1} } { 1- \dfrac {1} {\dfrac {1} {1-a} } } \] Wir dividieren durch einen Bruch im Nenner. \[ \dfrac { \dfrac {a} {a^2-1} } { 1+a-1} \] Wir vereinfachen den Nenner. \[ \dfrac { \dfrac {a} {a^2-1} } { a} \] Und schon sind wir durch. \[ \dfrac {1} {a^2-1} \] Die Aufgabe könnte auch mit der sogenannten Erweiterungsmethode gelöst werden \[ \dfrac { \dfrac {1} {a-\dfrac {1} {a} } } { 1- \dfrac {1} {1-\dfrac {1} {1-\dfrac {1} {a} } } } \] Wir erweitern den Bruch im Zähler und den Teilbruch im Nenner mit \(a\). \[ \dfrac { \dfrac {a} {a^2-a} } { 1- \dfrac {1} {1-\dfrac {a} {a-1 } } } \] Jetzt erweitern wir den Bruch im Nenner mit \((a-1)\). \[ \dfrac { \dfrac {a} {a^2-a} } { 1- \dfrac {a-1} {a-1-a} } \] Wir vereinfachen. \[ \dfrac { \dfrac {a} {a^2-a} } { 1- \dfrac {a-1} {-1} } \] Und vereinfachen nochmals. \[ \dfrac { \dfrac {a} {a^2-a} } {1-(1-a)} \] Und vereinfachen nochmals. \[ \dfrac { \dfrac {a} {a^2-a} } {a} \] Und schon sind wir wieder durch. \[ \dfrac {1} {a^2-1} \]
Erstellt von
Eugen Brigger
um
15:09
0
Kommentare

Diesen Post per E-Mail versendenBlogThis!In Twitter freigebenIn Facebook freigebenAuf Pinterest teilen
Labels:
A/027/064/b,
Algebra,
Aufgaben-gelöst,
BM,
Brüche,
Math,
Vorkurs
29.05.2011
Vektorgeometrie - Abstandsprobleme
Zu diesem Thema kann man sich folgende Aufgaben vorstellen. Berechnen
Sie den Abstand zwischen (gegeben):
Gegeben sind die Punkte \(A\left(1/2/5\right)\) und \(B\left (5/2/7\right)\). Bestimmen Sie den Abstand.
Wir bestimmen den Vektor \(\overrightarrow{AB}\) und berechnen seinen Betrag. \[ \overrightarrow{AB} = \begin{pmatrix} 5-1\\ 2-2\\ 7-5\\ \end{pmatrix} = \begin{pmatrix} 4\\ 0\\ 2\\ \end{pmatrix} \] Sein Betrag beträgt \[ \vert\overrightarrow{AB}\vert = \begin{vmatrix} \begin{pmatrix} 4\\ 0\\ 2\\ \end{pmatrix} \end{vmatrix} =\sqrt{4^2+0^2+2^2}=\sqrt{20}=2\sqrt{5} \] Abstand zwischen einem Punkt und einer Geraden.
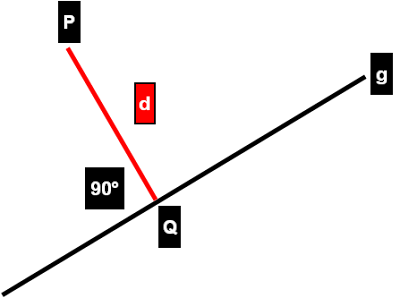
Gegeben sei der Punkt \(P\left(1/10/-1\right)\) und folgende Gerade. \[ g:\vec{r} = \begin{pmatrix} 1\\ 0\\ -2\\ \end{pmatrix} + t \begin{pmatrix} 2\\ 2\\ -3\\ \end{pmatrix} \] Wie weit ist P von der Geraden g entfernt (kürzester Abstand)?
Auch hier hilft eine kleine Skizze. Der Punkt \(Q\) liegt auf der Geraden g und hat somit folgende Koordinaten \[Q\left(1+2t/2t/-2-3t\right)\] Damit ergibt sich für den senktrechten Abstandsvektor \[ \overrightarrow{QP} = \begin{pmatrix} -2t\\ 10-2t\\ 1+3t\\ \end{pmatrix} \] Und wir können das Skalarprodukt formulieren \[ \overrightarrow{QP} \circ \begin{pmatrix} 2\\ 2\\ -3\\ \end{pmatrix} =-4t-4t-9t+20-3=-17t=-17 \Rightarrow t=1 \] Mit diesem t hat der Punkt Q die folgenden Koordianten \[Q\left(3/2/-5\right)\] Und für den Abstandsvektor erhalten wir \[ \overrightarrow{QP} = \begin{pmatrix} -2\\ 8\\ 4\\ \end{pmatrix} \] Und damit beträgt der gesuchte Abstand \[ d= \vert\overrightarrow{QP}\vert = \begin{vmatrix} \begin{pmatrix} -2\\ 8\\ 4\\ \end{pmatrix} \end{vmatrix} =\sqrt{2^2+8^2+4^2}=\sqrt{84}=2\sqrt{21} \] Abstand zwischen einem Punkt und einer Ebene.
Gegeben sei der Punkt \(P\left(1/10/-1\right)\) und folgende Ebene. \[E:x+2y+3z=4\] Wieder hilft uns eine Skizze. Wenn wir einen Schnitt zeichnen, kommen wir praktisch auf die gleiche Skizze wie bei der vorigen Aufgabe. Das Verfahren ist aber leicht verschieden.
Aus der Ebenengleichung gewinnen wir den Normalenvektor, also einen Vektor, der senkrecht auf der Ebene liegt. \[ \vec{n} = \begin{pmatrix} 1\\ 2\\ 3 \end{pmatrix} \] Damit können wir leicht die Gleichung der Geraden formulieren, die durch P geht und senkrecht zur Ebene verläuft. \[ g: \vec{r} \begin{pmatrix} 1\\ 10\\ -1 \end{pmatrix} +t \begin{pmatrix} 1\\ 2\\ 3 \end{pmatrix} \] Um den Punkt Q zu erhalten schneiden wir diese Gerade mit der Ebene. \[1+t+2\left(20+2t\right)+3\left(-1+3t\right)=4\] Damit erhalten wir das t, "mit dem man auf der Geraden von P nach Q reisen kann", in unserem Fall ist \(t=-1\)
Und so erhalten wir dann der Reihe nach die Koordinaten des Punktes Q, dann den Vektor \(\overrightarrow{QP}\) und am Schluss dessen Betrag. Wenn Sie richtig rechnen erhalten Sie \(d=\sqrt{14}\).
Abstand zwischen zwei windschiefen Geraden.
Gegeben sind die beiden folgenden Geraden. \[ g: \vec{r} \begin{pmatrix} 1\\ 0\\ 0 \end{pmatrix} +t \begin{pmatrix} 1\\ 2\\ 1 \end{pmatrix} \] \[ h: \vec{r} \begin{pmatrix} 0\\ 0\\ -1 \end{pmatrix} +s \begin{pmatrix} -1\\ 0\\ 2 \end{pmatrix} \] Dies ergibt für die Punkte \(P\) und \(Q\) die folgenden Koordinaten. \[P\left(-s/0/-1+2s\right)\qquad Q\left(1+t/2t/t\right)\] Der Vektor von \(P\) nach \(Q\) lautet dann \[ \overrightarrow{PQ}= \begin{pmatrix} 1+t+s\\ 2t\\ 1+t-2s \end{pmatrix} \] Und jetzt können wir zweimal das Skalarprodukt notieren. \[ \begin{align} \overrightarrow{PQ} \circ \begin{pmatrix} 1\\ 2\\ 1\\ \end{pmatrix} &= \begin{pmatrix} 1+t+s\\ 2t\\ 1+t-2s\\ \end{pmatrix} \circ \begin{pmatrix} 1\\ 2\\ 1\\ \end{pmatrix}\\ &=1+t+s+4t+1+t-2s=0 \end{align} \] \[ \Rightarrow 6t-s=-2 \] \[ \begin{align} \overrightarrow{PQ} \circ \begin{pmatrix} -1\\ 0\\ 2\\ \end{pmatrix} &= \begin{pmatrix} 1+t+s\\ 2t\\ 1+t-2s\\ \end{pmatrix} \circ \begin{pmatrix} -1\\ 0\\ 2\\ \end{pmatrix}\\ &=-1-t-s+2+2t-4s=0 \end{align} \] \[ \Rightarrow t-5s=-1 \] Womit wir zu einem Gleichungssystem mit zwei Gleichungen und zwei Unbekannten gekommen sind. Dies lässt sich auf eine der gelernten Arten lösen. Wir erhalten für s und t (bitte kontrollieren): \[s=\frac{4}{29}\quad\text{und}\quad t=-\frac{9}{29}\] Weiter erhält man mit etwas geschicktem Bruchrechnen
\[ \overrightarrow{PQ} = \frac{1}{29} \begin{pmatrix} 24\\ 18\\ 12 \end{pmatrix} \] Und damit als gesuchten Abstand d \[ \vert \overrightarrow{PQ}\vert=\frac{6}{\sqrt{29}} \] Die restlichen Aufgabentypen sollten nun keine Probleme mehr bieten.
- zwei Punkten
- einem Punkt und einer Geraden
- einem Punkt und einer Ebenen
- zwei Geraden
- einer Ebenen und einer parallelen Geraden
- zwei parallelen Ebenen
Gegeben sind die Punkte \(A\left(1/2/5\right)\) und \(B\left (5/2/7\right)\). Bestimmen Sie den Abstand.
Wir bestimmen den Vektor \(\overrightarrow{AB}\) und berechnen seinen Betrag. \[ \overrightarrow{AB} = \begin{pmatrix} 5-1\\ 2-2\\ 7-5\\ \end{pmatrix} = \begin{pmatrix} 4\\ 0\\ 2\\ \end{pmatrix} \] Sein Betrag beträgt \[ \vert\overrightarrow{AB}\vert = \begin{vmatrix} \begin{pmatrix} 4\\ 0\\ 2\\ \end{pmatrix} \end{vmatrix} =\sqrt{4^2+0^2+2^2}=\sqrt{20}=2\sqrt{5} \] Abstand zwischen einem Punkt und einer Geraden.
Gegeben sei der Punkt \(P\left(1/10/-1\right)\) und folgende Gerade. \[ g:\vec{r} = \begin{pmatrix} 1\\ 0\\ -2\\ \end{pmatrix} + t \begin{pmatrix} 2\\ 2\\ -3\\ \end{pmatrix} \] Wie weit ist P von der Geraden g entfernt (kürzester Abstand)?
Auch hier hilft eine kleine Skizze. Der Punkt \(Q\) liegt auf der Geraden g und hat somit folgende Koordinaten \[Q\left(1+2t/2t/-2-3t\right)\] Damit ergibt sich für den senktrechten Abstandsvektor \[ \overrightarrow{QP} = \begin{pmatrix} -2t\\ 10-2t\\ 1+3t\\ \end{pmatrix} \] Und wir können das Skalarprodukt formulieren \[ \overrightarrow{QP} \circ \begin{pmatrix} 2\\ 2\\ -3\\ \end{pmatrix} =-4t-4t-9t+20-3=-17t=-17 \Rightarrow t=1 \] Mit diesem t hat der Punkt Q die folgenden Koordianten \[Q\left(3/2/-5\right)\] Und für den Abstandsvektor erhalten wir \[ \overrightarrow{QP} = \begin{pmatrix} -2\\ 8\\ 4\\ \end{pmatrix} \] Und damit beträgt der gesuchte Abstand \[ d= \vert\overrightarrow{QP}\vert = \begin{vmatrix} \begin{pmatrix} -2\\ 8\\ 4\\ \end{pmatrix} \end{vmatrix} =\sqrt{2^2+8^2+4^2}=\sqrt{84}=2\sqrt{21} \] Abstand zwischen einem Punkt und einer Ebene.
Gegeben sei der Punkt \(P\left(1/10/-1\right)\) und folgende Ebene. \[E:x+2y+3z=4\] Wieder hilft uns eine Skizze. Wenn wir einen Schnitt zeichnen, kommen wir praktisch auf die gleiche Skizze wie bei der vorigen Aufgabe. Das Verfahren ist aber leicht verschieden.
Aus der Ebenengleichung gewinnen wir den Normalenvektor, also einen Vektor, der senkrecht auf der Ebene liegt. \[ \vec{n} = \begin{pmatrix} 1\\ 2\\ 3 \end{pmatrix} \] Damit können wir leicht die Gleichung der Geraden formulieren, die durch P geht und senkrecht zur Ebene verläuft. \[ g: \vec{r} \begin{pmatrix} 1\\ 10\\ -1 \end{pmatrix} +t \begin{pmatrix} 1\\ 2\\ 3 \end{pmatrix} \] Um den Punkt Q zu erhalten schneiden wir diese Gerade mit der Ebene. \[1+t+2\left(20+2t\right)+3\left(-1+3t\right)=4\] Damit erhalten wir das t, "mit dem man auf der Geraden von P nach Q reisen kann", in unserem Fall ist \(t=-1\)
Und so erhalten wir dann der Reihe nach die Koordinaten des Punktes Q, dann den Vektor \(\overrightarrow{QP}\) und am Schluss dessen Betrag. Wenn Sie richtig rechnen erhalten Sie \(d=\sqrt{14}\).
Abstand zwischen zwei windschiefen Geraden.
Gegeben sind die beiden folgenden Geraden. \[ g: \vec{r} \begin{pmatrix} 1\\ 0\\ 0 \end{pmatrix} +t \begin{pmatrix} 1\\ 2\\ 1 \end{pmatrix} \] \[ h: \vec{r} \begin{pmatrix} 0\\ 0\\ -1 \end{pmatrix} +s \begin{pmatrix} -1\\ 0\\ 2 \end{pmatrix} \] Dies ergibt für die Punkte \(P\) und \(Q\) die folgenden Koordinaten. \[P\left(-s/0/-1+2s\right)\qquad Q\left(1+t/2t/t\right)\] Der Vektor von \(P\) nach \(Q\) lautet dann \[ \overrightarrow{PQ}= \begin{pmatrix} 1+t+s\\ 2t\\ 1+t-2s \end{pmatrix} \] Und jetzt können wir zweimal das Skalarprodukt notieren. \[ \begin{align} \overrightarrow{PQ} \circ \begin{pmatrix} 1\\ 2\\ 1\\ \end{pmatrix} &= \begin{pmatrix} 1+t+s\\ 2t\\ 1+t-2s\\ \end{pmatrix} \circ \begin{pmatrix} 1\\ 2\\ 1\\ \end{pmatrix}\\ &=1+t+s+4t+1+t-2s=0 \end{align} \] \[ \Rightarrow 6t-s=-2 \] \[ \begin{align} \overrightarrow{PQ} \circ \begin{pmatrix} -1\\ 0\\ 2\\ \end{pmatrix} &= \begin{pmatrix} 1+t+s\\ 2t\\ 1+t-2s\\ \end{pmatrix} \circ \begin{pmatrix} -1\\ 0\\ 2\\ \end{pmatrix}\\ &=-1-t-s+2+2t-4s=0 \end{align} \] \[ \Rightarrow t-5s=-1 \] Womit wir zu einem Gleichungssystem mit zwei Gleichungen und zwei Unbekannten gekommen sind. Dies lässt sich auf eine der gelernten Arten lösen. Wir erhalten für s und t (bitte kontrollieren): \[s=\frac{4}{29}\quad\text{und}\quad t=-\frac{9}{29}\] Weiter erhält man mit etwas geschicktem Bruchrechnen
\[ \overrightarrow{PQ} = \frac{1}{29} \begin{pmatrix} 24\\ 18\\ 12 \end{pmatrix} \] Und damit als gesuchten Abstand d \[ \vert \overrightarrow{PQ}\vert=\frac{6}{\sqrt{29}} \] Die restlichen Aufgabentypen sollten nun keine Probleme mehr bieten.
Erstellt von
Eugen Brigger
um
11:59
0
Kommentare

Diesen Post per E-Mail versendenBlogThis!In Twitter freigebenIn Facebook freigebenAuf Pinterest teilen
28.05.2011
Vektorgeometrie - Ebenengleichung
DER INTERNET EXPLORER ZEIGT DIE FORMELN VIELLEICHT NICHT KORREKT AN.
Ich will hier zeigen, wie man zur Ebenengleichung kommt. Die Koordinatengleichung der Ebene lautet wie folgt. \[Ax+By+Cz=D\] Eine Ebene kann folgendermassen bestimmt sein.
Durch einen Punkt alleine ist die Ebene natürlich nicht definiert. Denken Sie an eine Balnacierscheibe, wie man sie in Parks findet, und an der Kinder Gefallen finden. Sobald ich aber einen zur Ebenen senkrechten Vektor habe, ist die Ebene fix (wie ein Regenschirm vielleicht).
Wenn ich vom Punkt P zu beliebigen Punkten Q auf der Ebene zeige, erhalte ich immer einen Vektor, der senkrecht zum gegebenen Vektor ist. Und damit können wir schnell das Skalarprodukt formulieren \[\vec{n}\circ\overrightarrow{PQ}=\begin{pmatrix}2\\1\\2\\\end{pmatrix}\begin{pmatrix}x-1\\y-6\\z-3\\\end{pmatrix}=2x+y+2z-14=0\] Damit haben wir auch die Ebenengleichung. \[2x+y+2z=14\] Auf das gleiche Resultat sollten wir stossen, wenn wir einen anderen Normalenvektor wählen, zum Beispiel einen, der doppelt so lang ist. Die Rechnung lautet dann folgendermassen: \[\vec{n_1}\circ\overrightarrow{PQ}=\begin{pmatrix}4\\2\\4\\\end{pmatrix}\begin{pmatrix}x-1\\y-6\\z-3\\\end{pmatrix}=4x+2y+4z-28=0\] Die Ebenengleichung wird damit einfach um 2 erweitert. Die Gleichung stellt aber die gleiche Ebene dar.
Was passiert, wenn wir einen anderen Punkt P vorgegeben haben, z.B. \(P_1=(1/6/2)\), aber den gleichen Normalenvektor? Es handelt sich also um eine zur obenen Ebene parallele Ebene.
Wieder rechnen wir das Skalarprodukt. \[\vec{n}\circ\overrightarrow{PQ}=\begin{pmatrix}2\\1\\2\\\end{pmatrix}\begin{pmatrix}x-1\\y-6\\z-2\\\end{pmatrix}=2x+y+2z-12=0\] Damit haben wir auch die Ebenengleichung. \[2x+y+2z=12\] Wir stellen also fest, dass uns die Koeffizienten A, B, C und D alle nötigen Informationen über die gegenseitige Lage von Ebenen liefern.
Ich will hier zeigen, wie man zur Ebenengleichung kommt. Die Koordinatengleichung der Ebene lautet wie folgt. \[Ax+By+Cz=D\] Eine Ebene kann folgendermassen bestimmt sein.
- durch drei Punkte
- durch zwei sich schneidende Geraden
- durch zwei parallele Geaden
- durch eine Gerade und einen Punkt
- durch einen Punkt und einen senkrechten Vektor auf der Ebenen
Durch einen Punkt alleine ist die Ebene natürlich nicht definiert. Denken Sie an eine Balnacierscheibe, wie man sie in Parks findet, und an der Kinder Gefallen finden. Sobald ich aber einen zur Ebenen senkrechten Vektor habe, ist die Ebene fix (wie ein Regenschirm vielleicht).
Wenn ich vom Punkt P zu beliebigen Punkten Q auf der Ebene zeige, erhalte ich immer einen Vektor, der senkrecht zum gegebenen Vektor ist. Und damit können wir schnell das Skalarprodukt formulieren \[\vec{n}\circ\overrightarrow{PQ}=\begin{pmatrix}2\\1\\2\\\end{pmatrix}\begin{pmatrix}x-1\\y-6\\z-3\\\end{pmatrix}=2x+y+2z-14=0\] Damit haben wir auch die Ebenengleichung. \[2x+y+2z=14\] Auf das gleiche Resultat sollten wir stossen, wenn wir einen anderen Normalenvektor wählen, zum Beispiel einen, der doppelt so lang ist. Die Rechnung lautet dann folgendermassen: \[\vec{n_1}\circ\overrightarrow{PQ}=\begin{pmatrix}4\\2\\4\\\end{pmatrix}\begin{pmatrix}x-1\\y-6\\z-3\\\end{pmatrix}=4x+2y+4z-28=0\] Die Ebenengleichung wird damit einfach um 2 erweitert. Die Gleichung stellt aber die gleiche Ebene dar.
Was passiert, wenn wir einen anderen Punkt P vorgegeben haben, z.B. \(P_1=(1/6/2)\), aber den gleichen Normalenvektor? Es handelt sich also um eine zur obenen Ebene parallele Ebene.
Wieder rechnen wir das Skalarprodukt. \[\vec{n}\circ\overrightarrow{PQ}=\begin{pmatrix}2\\1\\2\\\end{pmatrix}\begin{pmatrix}x-1\\y-6\\z-2\\\end{pmatrix}=2x+y+2z-12=0\] Damit haben wir auch die Ebenengleichung. \[2x+y+2z=12\] Wir stellen also fest, dass uns die Koeffizienten A, B, C und D alle nötigen Informationen über die gegenseitige Lage von Ebenen liefern.
Erstellt von
Eugen Brigger
um
12:27
0
Kommentare

Diesen Post per E-Mail versendenBlogThis!In Twitter freigebenIn Facebook freigebenAuf Pinterest teilen
26.05.2011
Gleichungssystem - lösen
DER INTERNET EXPLORER ZEIGT DIE FORMELN VIELLEICHT NICHT KORREKT AN.
Ich bin daran, mich in \(\TeX{}\) einzuarbeiten. Damit sollten meine Blog Einträge besser lesbar werden. Ich löse hier ein Gleichungssystem mit drei Unbekannten. Es handelt sich um folgende Aufgabe: A/131/411/a \[ \begin{align} x+y &=5-2z\tag{A}\\ x+z&=8-2y\tag{B}\\ 11-z&=2x+y\tag{C} \end{align} \] Zuerst ordnen wir neu. \[ \begin{align} x+y+2z &=5\tag{D} \\x+2y+z &=8\tag{E} \\2x+y+z &=11\tag{F} \end{align} \] Wir eliminieren \(x\), indem wir "D-E" und "2D-F" rechnen. \[ \begin{align} -y+z &=-3\tag{G}\\ y+3z &=-1\tag{H} \end{align} \] Wir eliminieren \(y\), indem wir "G+H" rechnen. \[ \begin{align} 4z &=-4\tag{I} \end{align} \]Damit ist \(z=-1\). \(y=2\) erhalten wir aus Gleichung H. Aus Gleichung D folgt dann \(x=5\). Die Lösung ist also \(\left(5/2/-1\right)\). Die Kontrolle sollte die Richtigkeit der Rechnung bestätigen. Die gefundenen Werte müssen die Gleichungen A, B und C erfüllen. Man kann die drei Gleichungen geometrisch als Ebenen auffassen. Sie schneiden sich in einem Punkt. Dies zeigt das folgende Bild.
Die Lösung des Gleichungssystems entspricht dem Schnittpunkt \(S=\left(5/2/-1\right)\). Hier noch die folgende Aufgabe: A/131/411/d \[\begin{align}3v+1&=4u+5w\\u-7w&=14-2v\\9w+1&=5v-6u\end{align}\]Zuerst ordnen wir neu.\[\begin{align}4u-3v+5w&=1\tag{A}\\u+2v-7w&=14\tag{B}\\6u-5v+9w&=-1\tag{C}\end{align}\]Wir eliminieren u, indem wir "A-4B" und "C-6B" rechnen.\[\begin{align}-11v+33w&=-55\tag{D}\\-17v+51w&=-85\tag{E}\end{align}\]Wir dividieren Gleichung D durch \(-11\) und Gleichung E durch \(17\).\[\begin{align}v-3w&=5\tag{D}\\-v+3w&=-5\tag{E}\end{align}\]Diese beiden Gleichungen sind äquivalent. Wir erhalten also als dritte Stufe:\[v-3w=5\tag{F}\]Das Gleichungssystem hat unendlich viele Lösungen. Wir schreiben \(w=\lambda\), wobei \(\lambda\in\mathbf{R}\). Aus Gleichung F folgt dann \(v=5+3\lambda\). u folgt aus Gleichung B.\[\begin{align}u&=14-2v+7w\\&=14-10-6\lambda+7\lambda\\&=4+\lambda\end{align}\]Und damit ist die Lösung:\[\left(\lambda+4/3\lambda+5/\lambda\right)\text{ mit }\lambda\in\mathbf{R}\]Wir interpretieren die drei Gleichungen wieder als Ebenengleichung und stellen diese graphisch dar. Man sieht dann, dass sich die Ebenen in einer Geraden schneiden.
Ich bin daran, mich in \(\TeX{}\) einzuarbeiten. Damit sollten meine Blog Einträge besser lesbar werden. Ich löse hier ein Gleichungssystem mit drei Unbekannten. Es handelt sich um folgende Aufgabe: A/131/411/a \[ \begin{align} x+y &=5-2z\tag{A}\\ x+z&=8-2y\tag{B}\\ 11-z&=2x+y\tag{C} \end{align} \] Zuerst ordnen wir neu. \[ \begin{align} x+y+2z &=5\tag{D} \\x+2y+z &=8\tag{E} \\2x+y+z &=11\tag{F} \end{align} \] Wir eliminieren \(x\), indem wir "D-E" und "2D-F" rechnen. \[ \begin{align} -y+z &=-3\tag{G}\\ y+3z &=-1\tag{H} \end{align} \] Wir eliminieren \(y\), indem wir "G+H" rechnen. \[ \begin{align} 4z &=-4\tag{I} \end{align} \]Damit ist \(z=-1\). \(y=2\) erhalten wir aus Gleichung H. Aus Gleichung D folgt dann \(x=5\). Die Lösung ist also \(\left(5/2/-1\right)\). Die Kontrolle sollte die Richtigkeit der Rechnung bestätigen. Die gefundenen Werte müssen die Gleichungen A, B und C erfüllen. Man kann die drei Gleichungen geometrisch als Ebenen auffassen. Sie schneiden sich in einem Punkt. Dies zeigt das folgende Bild.
Die Lösung des Gleichungssystems entspricht dem Schnittpunkt \(S=\left(5/2/-1\right)\). Hier noch die folgende Aufgabe: A/131/411/d \[\begin{align}3v+1&=4u+5w\\u-7w&=14-2v\\9w+1&=5v-6u\end{align}\]Zuerst ordnen wir neu.\[\begin{align}4u-3v+5w&=1\tag{A}\\u+2v-7w&=14\tag{B}\\6u-5v+9w&=-1\tag{C}\end{align}\]Wir eliminieren u, indem wir "A-4B" und "C-6B" rechnen.\[\begin{align}-11v+33w&=-55\tag{D}\\-17v+51w&=-85\tag{E}\end{align}\]Wir dividieren Gleichung D durch \(-11\) und Gleichung E durch \(17\).\[\begin{align}v-3w&=5\tag{D}\\-v+3w&=-5\tag{E}\end{align}\]Diese beiden Gleichungen sind äquivalent. Wir erhalten also als dritte Stufe:\[v-3w=5\tag{F}\]Das Gleichungssystem hat unendlich viele Lösungen. Wir schreiben \(w=\lambda\), wobei \(\lambda\in\mathbf{R}\). Aus Gleichung F folgt dann \(v=5+3\lambda\). u folgt aus Gleichung B.\[\begin{align}u&=14-2v+7w\\&=14-10-6\lambda+7\lambda\\&=4+\lambda\end{align}\]Und damit ist die Lösung:\[\left(\lambda+4/3\lambda+5/\lambda\right)\text{ mit }\lambda\in\mathbf{R}\]Wir interpretieren die drei Gleichungen wieder als Ebenengleichung und stellen diese graphisch dar. Man sieht dann, dass sich die Ebenen in einer Geraden schneiden.
Erstellt von
Eugen Brigger
um
13:53
0
Kommentare

Diesen Post per E-Mail versendenBlogThis!In Twitter freigebenIn Facebook freigebenAuf Pinterest teilen
Labels:
A/131/411/a,
A/131/411/d,
Algebra,
Aufgaben-gelöst,
BM,
Ebenen,
Gleichungssysteme,
Math
25.05.2011
Vektorgeometrie - Winkelberechnung
Wir nehmen wieder eine Aufgabe aus der Stereometrie, wo es darum geht, Winkel zwischen Ebenen und zwischen Geraden und Ebenen zu bestimmen, und schauen, ob sich die Vektorgeometrie dabei bewährt.
G/148/89
Alle Kanten einer vierseitigen Pyramide sind gleich lang. Berechnen Sie den Winkel zwischen
a) einer Seitenkante und der Grundfläche
b) einer Seitenfläche und der Grundfläche
c) zwei angrenzenden Seitenflächen
Wir erstellen eine Skizze und definieren ein Koordinatensysem.
Wir wählen eine Kantenlänge von 2 Einheiten.
Die Höhe lässt sich leicht über den Pythagoras berechnen.
Winkel zwischen einer Seitenkante und der Grundfläche
Dazu benötigen wir die folgenden Elemente.
Mit dem Skalarprodukt lässt sich der Winkel leicht berechnen.
Winkel zwischen einer Seitenfläche und der Grundfläche
Die Gleichung der Grundfläche und ihren Normalenvektor haben wir oben schon formuliert.
Für die Seitenfläche nehmen wir die Ebene durch die Punkte O, A und E.
Diese Ebene ist parallel zur x-Achse. z ist also nur von y abhängig. Ihre Koordinatengleichung und der entsprechende Normalenvektor lauten also:
Weiter geht es wieder mit dem Skalarprodukt. Man nimmt die Normalenvektoren der beiden Ebenen.
Winkel zwischen zwei angrenzenden Seitenflächen
Wir nehmen die Flächen links, die wir schon berechnet haben, und vorne.
Die Fläche vorne liegt auf einer Ebenen, die parallel zur y-Achse ist. In diesem Falle ist z eine Funktion von y. Wieder kommt man schnell zur Ebenengleichung und zum Normalenvektor.
Der Rest entspricht wieder dem Vorgehen von oben (Skalarprodukt der Normalenvektoren). Auch hier muss man sich wieder überlegen, welchen Winkel es zu nehmen gilt.
G/148/89
Alle Kanten einer vierseitigen Pyramide sind gleich lang. Berechnen Sie den Winkel zwischen
a) einer Seitenkante und der Grundfläche
b) einer Seitenfläche und der Grundfläche
c) zwei angrenzenden Seitenflächen
Wir erstellen eine Skizze und definieren ein Koordinatensysem.
Wir wählen eine Kantenlänge von 2 Einheiten.
Die Höhe lässt sich leicht über den Pythagoras berechnen.
Winkel zwischen einer Seitenkante und der Grundfläche
Dazu benötigen wir die folgenden Elemente.
Mit dem Skalarprodukt lässt sich der Winkel leicht berechnen.
Winkel zwischen einer Seitenfläche und der Grundfläche
Die Gleichung der Grundfläche und ihren Normalenvektor haben wir oben schon formuliert.
Für die Seitenfläche nehmen wir die Ebene durch die Punkte O, A und E.
Diese Ebene ist parallel zur x-Achse. z ist also nur von y abhängig. Ihre Koordinatengleichung und der entsprechende Normalenvektor lauten also:
Weiter geht es wieder mit dem Skalarprodukt. Man nimmt die Normalenvektoren der beiden Ebenen.
Winkel zwischen zwei angrenzenden Seitenflächen
Wir nehmen die Flächen links, die wir schon berechnet haben, und vorne.
Die Fläche vorne liegt auf einer Ebenen, die parallel zur y-Achse ist. In diesem Falle ist z eine Funktion von y. Wieder kommt man schnell zur Ebenengleichung und zum Normalenvektor.
Der Rest entspricht wieder dem Vorgehen von oben (Skalarprodukt der Normalenvektoren). Auch hier muss man sich wieder überlegen, welchen Winkel es zu nehmen gilt.
Erstellt von
Eugen Brigger
um
13:59
0
Kommentare

Diesen Post per E-Mail versendenBlogThis!In Twitter freigebenIn Facebook freigebenAuf Pinterest teilen
Labels:
Aufgaben-gelöst,
BM,
G/148/089,
Geometrie,
Gerade,
Stereometrie,
Vektoren,
Winkelberechnung
22.05.2011
Exponentielle Prozesse
Lösen wir ein paar konkrete Beispiele.
Beispiel - Zinseszins
Wenn man Geld auf die Bank bringt, erhält man dafür Zins - zwar nicht viel aber doch ein wenig. Der Zins wird dann zum Kapital geschlagen und auch verzinst - u.s.w. bis man alles Geld wieder abhebt.
Hier zuerst die Variablen, die wir in unserer Rechnung brauchen.
Jetzt berechnen wir das Kapital nach einem Jahr.
Das Kapital nach einem Jahr erhält man also, indem man das Anfangskapital mit q vermehrt.
Und da der Zins immer zum Kapital geschlagen wird, gilt entsprechend:
Das Kapital nach zwei Jahren erhält man, indem man das Kapital nach einem Jahr mit q vermehrt.
u.s.w.
Allgemein kann man formulieren:
Das neue Kapital erhält man, indem man das Kapital des Vorjahres mit q vermehrt.
Damit kommen wir zu der folgenden Formel für die Zinseszinsberechnung.
Zahlenbeispiel
Wie viel beträgt mein Kapital nach 10 Jahren wenn ich 2000 Franken zu 3% anlege?
Ich habe auch noch das Kapital nach 100 Jahren ausgerechnet. Mit Zinseszins ist es also leicht, reich und sogar Millionär zu werden. Dies wegen des exponentiellen Wachstums. Man muss nur lange genug warten. Die obige Rechnung ergibt für 1000 Jahre eine Zahl mit 17 Stellen. Diese Tatsache liefert denjenigen ein starkes Argument, die gegen jede Zinszahlung sind.
Zinssatz - Zinsfaktor
Es ist wichtig, dass man gut zwischen p und q unterscheidet. Siehe folgende Tabelle.
Hier eine Visualisierung mit GeoGebra. K, p und t können reguliert werden. Man sieht, dass die Kurve exponentiell ansteigt.
Beispiel - Blatt zerreissen
Jemand nimmt ein A4-Blatt Papier, reisst das Blatt mitten auseinander und legt die beiden Hälften aufeinander. Dann zerreisst er die beiden Hälften. Diesen Prozess wiederholt er fünfzig mal. Gegeben, dass ein Blatt Papier 0.07 mm dick ist, wie dick ist die Beige nach dem 50. Zerreissen?
Rechnen Sie selber und staunen Sie ob der Grösse der erhaltenen Zahl. Wie viele Erdumfänge gibt das?
Beispiel - Algenwachstum
Beispiel - Algenwachstum
Ein Algenpopulation im Genfersee nimmt eine Fläche von einem halben Quadratmeter ein. Sie verdreifacht sich alle vier Tage. Leiten Sie eine Formel für das Algenwachstum her.
Es geht also darum, eine Formel für die Fläche in Funktion der Zeit in Tagen zu finden.
Dies ist noch nicht die gewünschte Formel, denn "sie macht Vierersprünge".
Wir können durch Gleichsetzen der beiden Formeln q, den Wachstumsfaktor pro Tag, herausfinden.
Und damit lautet die gesuchte Formel:
MERKEN SIE SICH DIE BEDEUTUNG DER ZAHLEN 3 UND 4.
Erstellt von
Eugen Brigger
um
15:09
0
Kommentare

Diesen Post per E-Mail versendenBlogThis!In Twitter freigebenIn Facebook freigebenAuf Pinterest teilen
Labels:
BM,
Exponentialfunktionen,
exponentielle Prozesse,
Math
B E R G E
Alle Viertausender der Alpen
Öffne das Anwendungsfenster durch einen KLICK auf die folgende Schaltfläche. Wechsle dann in den VOLLBILDMODUS. Du benötigst vor allem den PFEIL und den DOPPELPFEIL in der WERKZEUGLEISTE. Mit einem RECHTSKLICK auf die Punkte kannst du die BESCHRIFTUNG einblenden. DREHEN DES MAUSRADES vergrössert die Ansicht. ZIEHEN MIT GEDRÜCKTEM MAUSRAD verschiebt die Ansicht.
Und dann
Welch ein Horror! - Wenn man Schüler im Englisch Unterricht frägt: What do you like doing on Sundays? - bekommt man oft Antworten wie:
- Schlafen
- Schlafen bis 14:00 Uhr
- Mit dem PC spielen (bis 22:00 Uhr)
- Im Zimmer sein
Als Idee hier ein Link zu meiner letzten Bergtour.
Grüebhorn im Baltschiedertal
 |
| Älwe Rigg - 3381 m ü. M. - bei der Baltschiederklause |
Erstellt von
Eugen Brigger
um
12:18
0
Kommentare

Diesen Post per E-Mail versendenBlogThis!In Twitter freigebenIn Facebook freigebenAuf Pinterest teilen
Labels:
Relax
Abonnieren
Posts (Atom)