Wir gehen von der allerseits bekannten Notenberechnung aus. Bei einem
Punktemaximum von 24 berechnet sich die Note wie folgt.
\[
\text{Note}=1+5\frac{\text{erreichte Punkte}}{\text{Punktemaximum}}
\]
abgekürzt
\[
N=1+5\frac{P}{24}
\]
Der entsprechende Graph sieht folgenderemassen aus.
Und genau so schaut ihn der Schüler in der ersten Schuljahreshälfte
auch an, das heisst, er schreibt einen Test, erhält dafür 17 Punkte,
und liest die Note ab - 4.5, wunderbar. Bei einigen ändert, vor allem
gegen Schuljahresende, die Perspektive. Plötzlich heisst es dann: im
nächsten Test brauche ich unbedingt eine 4.5, sonst bestehe ich das
Jahr nicht - wie viele Punkte muss ich erreichen? Der Schüler schaut
in dieser Phase den Graph also von links und nicht mehr von unten an.
Für den Schüler ist die Note jetzt die unabhängige und die Punktzahl
die abhängige Variable. Auch in seiner horizontalen Lage sieht er
natürlich ein Koordinatensystem, nur ist die Achsenbeschriftung nun
"irgendwie verkehrt" - für grössere Noten muss er sich nach links
wenden, für kleinere nach rechts. Und da diese Sichtweise etwas
ungewohnt ist, entscheidet sich der Schüler, das Koordinatensystem
wieder auf die übliche Art und Weise zu zeichnen. Das sieht dann wie
folgt aus.
Damit haben wir ausgehend von einer ersten Funktion ihre
Umkehrfunktion gezeichnet. Vielleicht kann man sich schon mal
überlegen, durch welche Abbildung (Verschiebung, Streckung,
Spiegelung) die Umkehrfunktion geometrisch aus der Funktion
hervorgeht.
Man kann sich auch den Definitions- und Wertebereich der beiden
Funktionen anschauen.
| Definitionsbereich | Wertebereich |
| Funktion | \(0\le \text{Punkte}\le 24\) | \(1\le \text{Note}\le 6\) |
| Umkehrfunktion | \(1\le \text{Note}\le 6\) | \(0\le \text{Punkte}\le
24\) |
Das Beispiel lässt vermuten, dass die Umkehrfunktion folgendermassen berechnet wird.
- Funktion nach x auflösen
- x und y vertauschen
Wir machen ein
Beispiel.
\[
y=\frac{1}{x}+2
\]
\[
\frac{1}{x}=y-2
\]
\[
x=\frac{1}{y-2}
\]
\[
\bar{y}=\frac{1}{x-2}
\]
Beachten Sie, wie die Umkehrfunktion bezeichnet wird (\(\bar{y}\)).
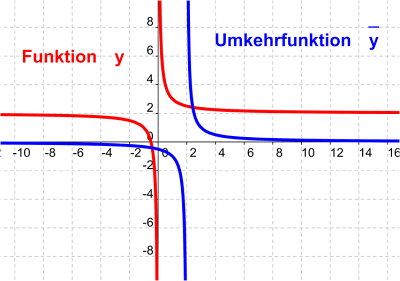
Hier der Graph
Die folgende Tabelle zeigt ein paar
Gesetzmässigkeiten.
|
Definitionsbereich |
Wertebereich |
Pol |
waagerechte Asymptote |
| \(y\) |
\(x \in \mathbf{R} \backslash x=0\) |
\(y \in \mathbf{R} \backslash y=2\) |
\(x=0\) |
\(y=2\) |
| \(\bar{y}\) |
\(x \in \mathbf{R} \backslash x=2\) |
\(y \in \mathbf{R} \backslash y=0\) |
\(x=2\) |
\(y=0\) |
Beachten Sie, dass Definitions- und Wertebereiche vertauscht sind, ebenso Pole und waagerechte Asymptoten.
Weiter ist feststellbar, dass Funktion und Umkehrfunktion spiegelbildlich zur 1. Winkelhalbierenden \(y=x\) liegen.
Es ist auch offensichtlich, dass die Umkehrfunktion der Umkehrfunktion wieder die Funktion ergibt. Die folgende
Rechnung bestätigt dies.
\[
y=\frac{1}{x-2}
\]
\[
(x-2)y=1
\]
\[
x-2=\frac{1}{y}
\]
\[
x=\frac{1}{y}+2
\]
\[
\bar{\bar{y}}=\frac{1}{x}+2=y
\]
Es gibt Funktionen, deren
Umkehrfunktion gleich der Funktion ist. Das einfachste Beispiel ist \(y=x\). Und die
folgende Rechnung zeigt das gleiche.
\[
y=\frac{1}{x}
\]
\[
x=\frac{1}{y}
\]
\[
\bar{y}=\frac{1}{x}=y
\]
Nur Funktionen sind umkehrbar. \(x=10\) ist keine Funktion, und daher nicht umkehrbar. Und dies, obwohl der
Graph von \(x=10\) von der y-Achse aus betrachtet wie eine Funktion aussieht.
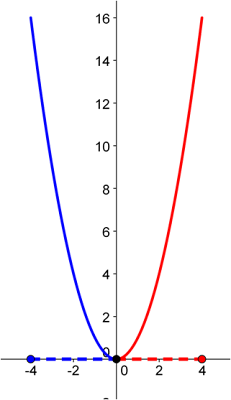
Und dann gibt es noch Funktionen, die nur umkehrbar sind, wenn man ihren Definitionsbereich einschränkt. Sie sind also
nur auf gewissen
Intervallen umkehrbar. Das einfachste Beispiel ist \(y=x^2\).
Von der x-Achse aus betrachtet, haben wir es hier natürlich mit einer Funktion zu tun (jedem x-Wert ist ein und nur
ein y-Wert zugeordnet). Wenn wir den Graph aber von der y-Achse aus anschauen, ist es keine Funktion mehr (es gibt y-
Werte, denen mehr als ein (nämlich 2) x-Werte zugeordnet sind).
Wir können aber die Umkehrfunktion bilden, wenn wir den Definitionsbereich einschränken, z.B. \(0\le x \le 4\). Wir
kehren also nur einen "Ast" der Funktion um.
\[
y=x^2
\]
\[
x=+\sqrt{y}
\]
\[
\bar{y}=+\sqrt{x}
\]
Auch hier beachte man, wie Definitions- und Wertebereich ihre Rollen tauschen. Entsprechend könnte man natürlich den blauen Ast umkehren.
