Zu diesem Thema kann man sich folgende Aufgaben vorstellen. Berechnen
Sie den Abstand zwischen (gegeben):
- zwei Punkten
- einem Punkt und einer Geraden
- einem Punkt und einer Ebenen
- zwei Geraden
- einer Ebenen und einer parallelen Geraden
- zwei parallelen Ebenen
Abstand zwischen zwei Punkten.
Gegeben sind die Punkte \(A\left(1/2/5\right)\) und \(B\left
(5/2/7\right)\). Bestimmen Sie den Abstand.
Wir bestimmen den Vektor \(\overrightarrow{AB}\) und berechnen seinen
Betrag.
\[
\overrightarrow{AB}
=
\begin{pmatrix}
5-1\\
2-2\\
7-5\\
\end{pmatrix}
=
\begin{pmatrix}
4\\
0\\
2\\
\end{pmatrix}
\]
Sein Betrag beträgt
\[
\vert\overrightarrow{AB}\vert
=
\begin{vmatrix}
\begin{pmatrix}
4\\
0\\
2\\
\end{pmatrix}
\end{vmatrix}
=\sqrt{4^2+0^2+2^2}=\sqrt{20}=2\sqrt{5}
\]
Abstand zwischen einem Punkt und einer Geraden.
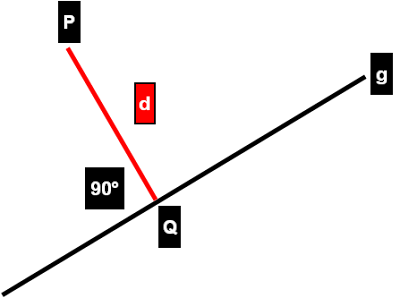
Gegeben sei der Punkt \(P\left(1/10/-1\right)\) und folgende Gerade.
\[
g:\vec{r}
=
\begin{pmatrix}
1\\
0\\
-2\\
\end{pmatrix}
+
t
\begin{pmatrix}
2\\
2\\
-3\\
\end{pmatrix}
\]
Wie weit ist P von der Geraden g entfernt (kürzester Abstand)?
Auch hier hilft eine kleine Skizze.
Der Punkt \(Q\) liegt auf der Geraden g und hat somit folgende
Koordinaten
\[Q\left(1+2t/2t/-2-3t\right)\]
Damit ergibt sich für den senktrechten Abstandsvektor
\[
\overrightarrow{QP}
=
\begin{pmatrix}
-2t\\
10-2t\\
1+3t\\
\end{pmatrix}
\]
Und wir können das Skalarprodukt formulieren
\[
\overrightarrow{QP}
\circ
\begin{pmatrix}
2\\
2\\
-3\\
\end{pmatrix}
=-4t-4t-9t+20-3=-17t=-17
\Rightarrow t=1
\]
Mit diesem t hat der Punkt Q die folgenden Koordianten
\[Q\left(3/2/-5\right)\]
Und für den Abstandsvektor erhalten wir
\[
\overrightarrow{QP}
=
\begin{pmatrix}
-2\\
8\\
4\\
\end{pmatrix}
\]
Und damit beträgt der gesuchte Abstand
\[
d=
\vert\overrightarrow{QP}\vert
=
\begin{vmatrix}
\begin{pmatrix}
-2\\
8\\
4\\
\end{pmatrix}
\end{vmatrix}
=\sqrt{2^2+8^2+4^2}=\sqrt{84}=2\sqrt{21}
\]
Abstand zwischen einem Punkt und einer Ebene.
Gegeben sei der Punkt \(P\left(1/10/-1\right)\) und folgende Ebene.
\[E:x+2y+3z=4\]
Wieder hilft uns eine Skizze. Wenn wir einen Schnitt zeichnen, kommen
wir praktisch auf die gleiche Skizze wie bei der vorigen Aufgabe.
Das Verfahren ist aber leicht verschieden.
Aus der Ebenengleichung gewinnen wir den Normalenvektor, also einen
Vektor, der senkrecht auf der Ebene liegt.
\[
\vec{n}
=
\begin{pmatrix}
1\\
2\\
3
\end{pmatrix}
\]
Damit können wir leicht die Gleichung der Geraden formulieren, die
durch P geht und senkrecht zur Ebene verläuft.
\[
g:
\vec{r}
\begin{pmatrix}
1\\
10\\
-1
\end{pmatrix}
+t
\begin{pmatrix}
1\\
2\\
3
\end{pmatrix}
\]
Um den Punkt Q zu erhalten schneiden wir diese Gerade mit der Ebene.
\[1+t+2\left(20+2t\right)+3\left(-1+3t\right)=4\]
Damit erhalten wir das t, "mit dem man auf der Geraden von P nach Q
reisen kann", in unserem Fall ist \(t=-1\)
Und so erhalten wir dann der Reihe nach die Koordinaten des Punktes Q,
dann den Vektor \(\overrightarrow{QP}\) und am Schluss dessen Betrag.
Wenn Sie richtig rechnen erhalten Sie \(d=\sqrt{14}\).
Abstand zwischen zwei windschiefen Geraden.
Gegeben sind die beiden folgenden Geraden.
\[
g:
\vec{r}
\begin{pmatrix}
1\\
0\\
0
\end{pmatrix}
+t
\begin{pmatrix}
1\\
2\\
1
\end{pmatrix}
\]
\[
h:
\vec{r}
\begin{pmatrix}
0\\
0\\
-1
\end{pmatrix}
+s
\begin{pmatrix}
-1\\
0\\
2
\end{pmatrix}
\]
Dies ergibt für die Punkte \(P\) und \(Q\) die folgenden Koordinaten.
\[P\left(-s/0/-1+2s\right)\qquad Q\left(1+t/2t/t\right)\]
Der Vektor von \(P\) nach \(Q\) lautet dann
\[
\overrightarrow{PQ}=
\begin{pmatrix}
1+t+s\\
2t\\
1+t-2s
\end{pmatrix}
\]
Und jetzt können wir zweimal das Skalarprodukt notieren.
\[
\begin{align}
\overrightarrow{PQ}
\circ
\begin{pmatrix}
1\\
2\\
1\\
\end{pmatrix}
&=
\begin{pmatrix}
1+t+s\\
2t\\
1+t-2s\\
\end{pmatrix}
\circ
\begin{pmatrix}
1\\
2\\
1\\
\end{pmatrix}\\
&=1+t+s+4t+1+t-2s=0
\end{align}
\]
\[
\Rightarrow 6t-s=-2
\]
\[
\begin{align}
\overrightarrow{PQ}
\circ
\begin{pmatrix}
-1\\
0\\
2\\
\end{pmatrix}
&=
\begin{pmatrix}
1+t+s\\
2t\\
1+t-2s\\
\end{pmatrix}
\circ
\begin{pmatrix}
-1\\
0\\
2\\
\end{pmatrix}\\
&=-1-t-s+2+2t-4s=0
\end{align}
\]
\[
\Rightarrow t-5s=-1
\]
Womit wir zu einem Gleichungssystem mit zwei Gleichungen und zwei
Unbekannten gekommen sind. Dies lässt sich auf eine der gelernten
Arten lösen. Wir erhalten für s und t (bitte kontrollieren):
\[s=\frac{4}{29}\quad\text{und}\quad t=-\frac{9}{29}\]
Weiter erhält man mit etwas geschicktem Bruchrechnen
\[
\overrightarrow{PQ}
=
\frac{1}{29}
\begin{pmatrix}
24\\
18\\
12
\end{pmatrix}
\]
Und damit als gesuchten Abstand d
\[
\vert \overrightarrow{PQ}\vert=\frac{6}{\sqrt{29}}
\]
Die restlichen Aufgabentypen sollten nun keine Probleme mehr bieten.
