Planimetrie - Kreisberechnung

Folgende Formeln für die Berechnung des Umfangs und der Fläche des Kreises sollten bekannt sein. $$\begin{align} U&=2r\pi=d\pi\\ A&=r^2\pi \end{align}$$ Alle Kreise sind einander ähnlich, d.h. sie gehen durch eine zentrische Streckung auseinander hervor. Daher gilt für alle Kreise $$\frac{u}{2r}=const=\pi$$ Über die Zahl $\pi$ gäbe es viel zu berichten und zu lesen. Ich verweise diesbezüglich zum Beispiel auf WIKIPEDIA und wünsche eine spannende Feierabendlektüre. Wir wenden uns hier zwei wichtigen Berechnungen zu.

Flächen- und Umfangberechnung

Fläche und Umfang des Kreises können mit einfachen Methoden der Geometrie annäherungsweise berechnet werden.

Prinzip: Wir beschreiben dem Kreis regelmässige Vielecke ein und erhöhen schrittweise deren Seitenzahl. Je mehr Seiten das Vieleck hat, desto weniger unterscheidet sich seine Fläche von der Fläche des Kreises. Entsprechend können wir dem Kreis Vielecke umbeschreiben. Ich mache hier die Berechnung für ein- und umbeschriebene Vier- und Achtecke, und überlasse es dem Schüler, bis zum 1024-Eck weiterzurechnen.

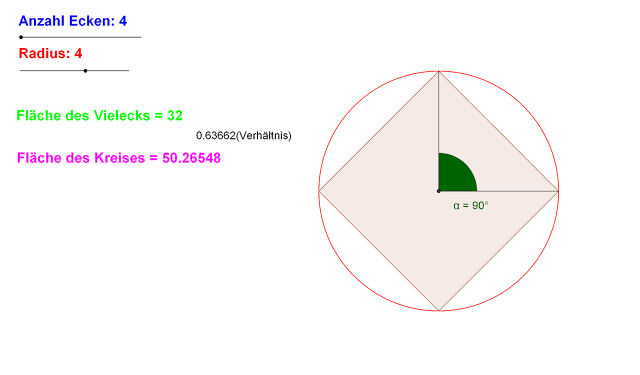
Quadrat

Bei einem Kreisradius $r=4$
beträgt die Quadratseite $\sqrt{2}r=\sqrt{2}\cdot4$
und die Fläche des Quadrates $(\sqrt{2}r)^2=2r^2=2\cdot16=32$
Die Abweichung geht aus dem Bild hervor.

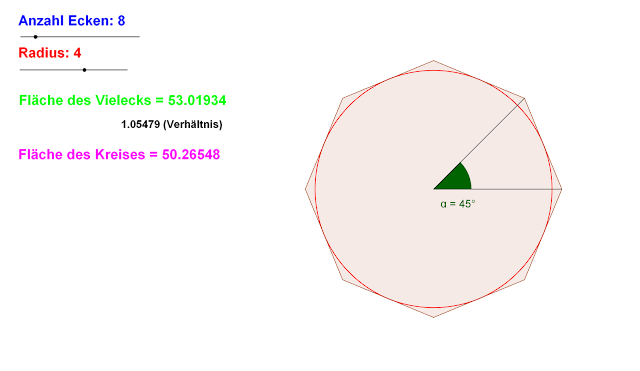
Achteck

Hier benutzen wir die Formel für die Berechnung der Dreiecksfläche.

$$\begin{align} 8A_\vartriangle&=8\frac{1}{2}r^2\sin45^\circ\\ 8A_\vartriangle&=8\frac{1}{2}16\frac{1}{\sqrt{2}}\\ 8A_\vartriangle&=\frac{64}{\sqrt{2}}\\ 8A_\vartriangle&\approx45.2548 \end{align}$$ Die Abweichung von der Kreisfläche ist schon viel geringer.

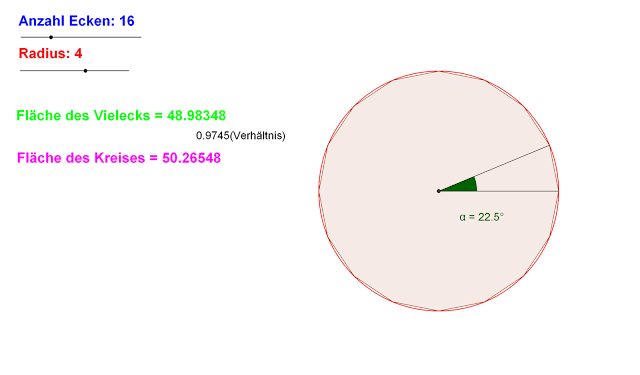
Sechzehneck

Auch hier können wir wieder sehr gut mit der eben benutzten Sinusformel für die Berechnung der Dreiecksfläche arbeiten.

Jetzt noch die GeoGebra Applikation zum Weiter-Experimentieren. Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser (Click here to install Java now) Hier folgen jetzt noch die Bilder für die Berechnung der umschreibenden Vielecke. Wieder kann leicht vom Kreisradius r ausgegangen werden. Am Schluss folgt wieder die GeoGebra Applikation zum Experimentieren.

 

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser (Click here to install Java now) Auf ähnliche Weise, wie wir es für die Fläche getan haben, könnte man den Kreisumfang approximieren.

Einer unserer Vorahnen war drauf und dran, das Rad zu erfinden. In einem Anflug schöpferischer Intuition hatte er aus Holz ein Sechzehneck konstruiert. Er klagte sich bei seinem Kollegen (einem Nichtmathematiker), dass das Rad nun bei jeder Umdrehung sechzehnmal tag-tag-tag... mache und die Passagiere ganz gehörig durchschüttle. Dieser, wie gesagt ein Nichmathematiker, riet ihm, ein viereckiges Rad zu schaffen, dann mache es nur noch viermal tag-tag-tag...