Stereometrie - Formeln zum Lernen

Was hier folgt, sollte man auswendig wissen.

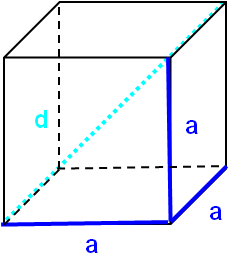
Würfel

Alle Seiten sind gleich lang.
Alle Begrenzungsflächen sind Quadrate.

\[\text{Oberfläche:}\qquad O=6a^2\] \[\text{Volumen:}\qquad V=a^3\] \[\text{Körperdiagonale:}\qquad=\sqrt{3}a\] Quader

Seiten sind unterschiedlicher Länge (Länge, Breite, Höhe).
Begrenzungsflächen sind Rechtecke.

\[\text{Oberfläche:}\qquad O=2(lb+lh+bh)\] \[\text{Volumen:}\qquad V=l\cdot b\cdot h\] \[\text{Körperdiagonale:}\qquad=\sqrt{l^2+b^2+h^2}\] Prisma

Würfel und Quader sind Beispiele von Prismen.
Prismen sind begrenzt von 2 kongruenten und parallelen n-Ecken (Grund- und Deckfläche).
Der Mantel besteht aus Parallelogrammen.
Beim geraden Prisma besteht der Mantel ausschliesslich aus Rechtecken.
Beim regulären Prisma ist die Grundfläche ein reguläres Vieleck.

Hier ein paar reguläre Prismen.
Und ein nicht reguläres Prisma.

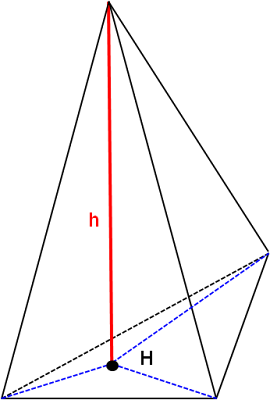
Pyramide

Die Grundfläche ist ein Vieleck (regelmässig oder nicht regelmässig).
Die Seiten werden von Dreiecken gebildet.

\[\text{Oberfläche:}\qquad S=M+G\] Die Oberfläche S wird von der Mantelfläche (Summe aller Seitenflächen) und der Grundfläche gebildet. \[\text{Volumen:}\qquad V=\frac{1}{3}G\cdot h\] Bei der geraden Pyramide fällt der Fusspunkt der Höhe h mit dem Schwerpunkt der Grundfläche zusammen.
Bei der regulären Pyramide ist die Grundfläche ein regelmässiges Vieleck.
Beim Tetraeder ist die Grundfläche ein Dreieck.
Ein reguläres Tetraeder besteht aus vier gleichseitigen Dreiecken.

Zylinder

Grund- und Deckflächen sind Kreise.
Es gibt gerade und schiefe Kreiszylinder.
Rollt man einen Zylinder ab, entsteht ein Rechteck (Abwicklung).
\[\text{Oberfläche:}\qquad S=G+D+M=r^2\pi+r^2\pi+2r\pi h = 2r\pi(r +h)\] \[\text{Volumen:}\qquad V=G\cdot h=r^2\pi h\] Kreiskegel

Ohne nähere Beschreibung sieht ein gerader Kreiskegel wie folgt aus.

Es ist auch der abgewickelte Mantel eingezeichnet worden.
Wichtige Begriffe sind:

• Mantellinie m
• abgewickelter Mantel
• Öffnungswinkel \(\alpha\)
• Zentriwinkel des abgewickelten Mantels \(\varphi\)

Das Volumen berechnet sich wie bei der Pyramide. \[\text{Volumen:}\qquad V=\frac{1}{3}G\cdot h=\frac{1}{3}r^2\pi h\] Für die Berechnung der Mantelfläche M betrachten wir den abgewickelten Mantel. Dies ist offensichtlich ein Kreissektor mit Radius \(m\) und einem Zentriwinkel von \(2r\pi\) im Bogenmass. Also gilt für seine Fläche \[ \begin{align} M &= \frac{m^2 \pi \cdot 2r\pi}{2rm}\\ &=\color{red}{\pi rm} \end{align} \] Denken Sie an die ersten vier Buchstaben von PIRMIN. Damit ist die Formel für die Berechnung der Oberfläche S \[ S=G+M=r^2\pi+\pi rm=\pi r(r+m) \] Nützlich ist auch die folgende Formel. \[ \begin{align} \frac{\varphi}{360^\circ} &= \frac{2r \pi}{2m \pi}\\ \frac{\varphi}{360^\circ} &= \frac{r}{m} \end{align} \] Der Radius r des Kegels verhält sich also zur Mantellinie m, wie sich der Zentriwinkel des abgewickelten Mantels zu 360 Grad verhält.